Diseña tu propia "Misión a Marte"
Desde que el cine de ciencia ficción es el cine de ciencia ficción, los guionistas han tenido una relación muy especial con Marte, el cuarto planeta desde el Sol. Decenas de películas tienen, de una manera u otra, al planeta rojo como protagonista. Y no digamos ya a sus hipotéticos habitantes, los marcianos. Clásicos como Cohete K-1 (Rocketship X-M, 1950), donde una nave espacial con rumbo a la Luna se ve desviada de su trayectoria por una lluvia de meteoritos, dirigiéndose ahora hacia Marte; Flight to Mars (1951), donde los meteoritos vuelven a hacer de las suyas; Los invasores de Marte (Invaders from Mars, 1953), The Angry Red Planet (1959) y otras mucho más recientes, como Planeta rojo (Red Planet, 2000) o Misión a Marte (Mission to Mars, 2000) no constituyen más que una pequeña muestra de lo que Hollywood ha aportado a uno de los mayores sueños del ser humano: el viaje a nuestro mundo vecino. Aunque lo más usual cuando se está hablando de una hipotética misión a Marte es referirse a un viaje tanto de ida como de vuelta, lo cierto es que esto no tiene por qué ser así necesariamente. De hecho, hace tan sólo unos días saltaba la noticia de que los doctores Dirk Schulze-Makuch y Paul Davies han propuesto la original idea de enviar una tripulación al planeta rojo que no regresaría, permaneciendo para siempre sobre la superficie de Marte. La idea inicial consistiría en lanzar dos naves espaciales con dos astronautas en cada una de ellas. Una vez en su destino, deberían ser capaces de autoabastecerse y comenzar con la colonización, que continuaría con otras futuras misiones.
Pero no es éste el tema al que yo me quiero referir en esta entrada. Como seguramente sabréis, hoy se han publicado los nombres de los blogs finalistas en los Premios Bitácoras.com 2010 y Física en la Ciencia Ficción ha resultado elegido en dos de las tres categorías en las que se presentaba. Se trata de Educación y Ciencia. Y con este motivo quiero contaros aquí y ahora algo que tiene que ver con las dos máximas de este blog. Nada más y nada menos pretendo que enseñaros cómo se diseña, a grandes rasgos, una misión de ida y vuelta al planeta Marte. Como enseguida comprobaréis, será un post tremendamente educativo y muy asequible con el que, además, aprenderéis ciencia de la forma que caracteriza a este blog. Por supuesto, no es el objetivo de esta entrada diseñar la expedición con pelos y señales, pues sabéis que siempre he mantenido la idea de la sencillez, de la comprensión por parte de todos aquellos que tengan un nivel de física y/o matemáticas intermedio. Ciencia al alcance de todos. Lo que deseo es que con lo que leáis os pique el gusanillo de la curiosidad y os animéis a aprender más, a descubrir por vosotros mismos, a ir más allá de donde yo os dejaré. No hay mayor placer intelectual que el proporcionado por los propios descubrimientos. Así, pues, sentaos y ajustad vuestros cinturones. Partimos rumbo a Marte...
Y para ello voy a hacer uso de una frase que se puede escuchar en la última de las películas a las que hacía referencia en el primer párrafo: Misión a Marte (Mission to Mars, 2000). Al principio del metraje, los miembros de la tripulación celebran una fiesta de despedida del planeta Tierra. En un momento dado, uno de los miembros, Nicholas Willis, intenta convencer a una chica de que su último día en este planeta sería mucho más divertido si... En fin, que se acerca a ella y le dice lo siguiente:
Verás, se tarda seis meses en llegar a Marte. Luego, un año allí y seis meses de vuelta son dos años, ¿sabes?
Bien, lo que haré a continuación será mostraros con unos cuantos conceptos y principios de física básica cuán acertada o cuán alejada de la realidad es la frase anterior. Para ello, haré antes unas cuantas suposiciones simplificadoras. En caso contrario, el problema se complicaría en exceso y sería necesario acudir a una simulación numérica con ayuda de una computadora. Al final, veréis que la diferencia entre nuestra solución y la que aporta la mismísima NASA no difieren demasiado. Dichas suposiciones simplificadoras consisten en suponer que las órbitas de la Tierra y de Marte son circulares (con el Sol situado en su centro), así como coplanarias (los planos de ambas forman tan sólo un ángulo de 1,8º); también se desprecian las interacciones gravitatorias entre la nave y los dos planetas, así como con sus atmósferas a la salida y a la llegada.
Uno de los requisitos básicos a la hora de lanzar una misión espacial es el presupuesto, ya que la millonada es para echarse a temblar; de hecho puede superar el producto interior bruto de muchos países y únicamente las grandes naciones económicamente muy poderosas pueden afrontarlo. Por lo tanto, conviene minimizar el consumo energético durante el periplo. Daos cuenta que se pretende poner en órbita marciana un vehículo espacial que parte de la Tierra. No consideraré otras posibilidades, como pueden ser colocar la nave en la Luna o en otra base cualquiera exterior a la Tierra y hacerla partir desde ella. Así pues el problema técnico consiste en transferir desde una órbita baja (la de la Tierra, desde el punto de vista del Sol) a otra órbita alta (la de Marte, también vista desde el Sol). ¿Cómo hacerlo?
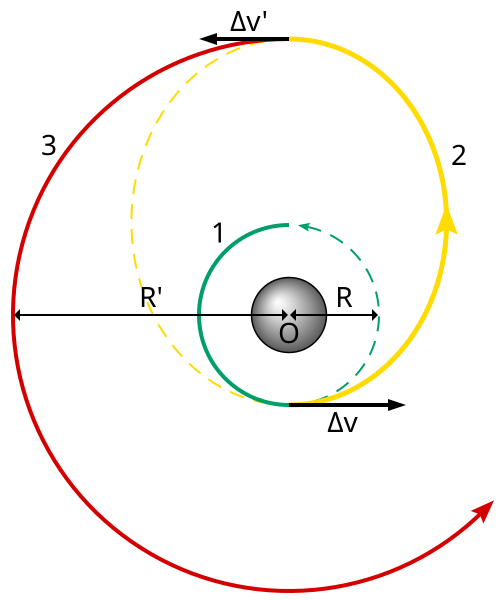
Pues a fuerza de ser sincero, lo anterior se puede llevar a cabo de muchas formas distintas. Ahora bien, una posibilidad a tener muy en cuenta consiste en seguir el procedimiento descubierto por el ingeniero alemán Walter Hohmann en 1925. En efecto, Hohmann consiguió demostrar que existía una manera de "saltar" de una órbita baja a otra alta consumiendo para ello la cantidad de energía más pequeña posible. Esta técnica se denomina órbita de transferencia de Hohmann y consiste, en el caso del viaje Tierra-Marte, en partir desde el primero y alcanzar el segundo cuando éste se encuentra a 180º con respecto a la posición inicial de la Tierra, justo al otro lado del Sol. Hay que tener en cuenta que lo anterior implica que la Tierra y Marte deben estar en una posición relativa muy particular, ya que mientras la nave está viajando los dos planetas se habrán desplazado ángulos diferentes a causa de sus distintas velocidades orbitales (29,8 km/s y 24,1 km/s, respectivamente). Veamos cómo determinar el ángulo que deben formar los radios de las dos órbitas planetarias en el momento del lanzamiento del vehículo espacial.
En primer lugar, necesitaré conocer el período de la órbita de Hohmann, es decir, el tiempo empleado por la sonda en el viaje de ida más el de vuelta. La 3ª ley de Kepler acude en mi rescate: "el cuadrado del período orbital es directamente proporcional al cubo del semieje mayor de la órbita". La constante de proporcionalidad entre ambos parámetros es la misma para todos los planetas del Sistema Solar y tiene un valor de 1 año2/UA3 (UA significa Unidad Astronómica, la distancia media de la Tierra al Sol, de unos 150 millones de kilómetros). Si se observa con atención el esquema de la figura, se ve fácilmente que el radio de la órbita de Hohmann es el valor medio entre los radios de las órbitas de la Tierra y Marte. Como éstos resultan ser de 1 UA y 1,52 UA, respectivamente, el de la nave será 1,26 UA. Así, deducimos que la nave empleará casi 517 días en recorrer su órbita, algo más de 258 días en cada sentido (más de 8 meses y medio).
En estos 258 días, la nave ha descrito un ángulo de 180º a lo largo de su órbita. Durante ese mismo tiempo, Marte solamente habrá recorrido poco más de 135º (recordad que su velocidad orbital es de 24,1 km/s y su período de 687 días). En consecuencia, y restando ambos desplazamientos angulares, se llega a que las posiciones de los dos planetas, la Tierra y Marte, deben ser tales que el segundo se adelante algo más de 44º con respecto al primero (la Tierra viaja más rápido en su órbita que Marte, dado que está más próxima al Sol).
El siguiente detalle importante consiste en conocer tanto la velocidad con la que es preciso lanzar la nave espacial desde la superficie de la Tierra, como la requerida en el momento de regresar desde la superficie del planeta rojo. Ambas se pueden determinar de forma muy simple acudiendo a otras dos leyes básicas de la física newtoniana. Se trata de la conservación de la energía mecánica y de la conservación del momento angular. Las dos relacionan las velocidades del vehículo espacial con sus distancias respectivas máxima y mínima al Sol (afelio y perihelio). Dicho en otras palabras y quizá más comprensibles: como tanto la energía mecánica como el momento angular siempre conservan un valor constante, podemos tomar estos valores e igualarlos en dos puntos muy concretos, el de máximo alejamiento entre la nave y el Sol (afelio, que coincide con el punto donde la nave se encuentra con Marte) y el de máximo acercamiento de la nave al Sol (perihelio, que coincide con el punto en que la nave abandona la Tierra). Resolviendo este sistema de dos ecuaciones con dos incógnitas, surgen las dos velocidades buscadas: 32,8 km/s en el lanzamiento y 21,6 km/s al llegar a las proximidades de Marte. Hay que tener en cuenta que dichas velocidades son con respecto al Sol y no a cada uno de los dos planetas de origen y destino.
La importancia del cálculo de las dos velocidades anteriores se ve a la hora de establecer el consumo de energía a lo largo de toda la órbita, lo que determina de alguna manera el presupuesto de la misión. Como bien sabéis, una vez que la nave alcanza la velocidad orbital no se requieren los motores de la misma encendidos (en el espacio interplanetario la velocidad del vehículo se mantienen constante como consecuencia de la 1ª ley de Newton), accionándose aquellos únicamente cuando se precisa corregir la órbita, frenar o acelerar. Y estos cambios en la velocidad (conocidos como "delta de v") son los que consumen energía. Así pues, dado que la velocidad orbital de la Tierra es de 29,8 km/s y que la que la nave en su perihelio necesita alcanzar asciende hasta los 32,8 km/s, ésta debe incrementar su velocidad en 32,8 - 29,8 = 3 km/s. A esto hay que añadir la velocidad de escape en la superficie de la Tierra, unos 11,2 km/s, ya que os recuerdo que las velocidades anteriores se refieren todas ellas al Sol. El cambio total en la velocidad de la nave espacial en el momento del inicio de la misión asciende a 11,2 + 3 = 14,2 km/s. Cuando, finalmente, se esté aproximando a Marte, hay que tener en cuenta que su velocidad de aproximación (21,6 km/s) es inferior a la velocidad orbital del planeta (24,1 km/s) y, por tanto, la posición de la nave deberá ser ligeramente adelantada, con el objeto de que Marte la alcance. En ese preciso momento se activarán los retropropulsores y se adaptarán las velocidades orbitales de ambos cuerpos, sin olvidarnos de la velocidad de escape en la superficie de Marte, que resulta ser de unos 5,1 km/s. El delta de v correspondiente a la llegada asciende hasta 5,1 + (24,1 - 21,6) = 7,6 km/s. En total, para todo el viaje de ida 21,8 km/s. Precisamente lo que hace a la órbita de transferencia de Hohmann tan interesante es que cualquier otra alternativa que se idease llevaría asociada una delta de v siempre mayor que la determinada anteriormente.
En lo que respecta al viaje de vuelta, resulta obvio que su duración será idéntica a la del periplo de ida, esto es, otros 258 días terrestres. Ahora bien, la orientación entre Marte y la Tierra debe ser nuevamente la adecuada. Ahora lo que hay que determinar es el desplazamiento angular que ha recorrido nuestro planeta durante esos 258 días. Procediendo de forma análoga a como hicimos con Marte durante el viaje de ida, se llega fácilmente a que dicho ángulo recorrido asciende hasta los 255º. Consecuentemente, la nave debe abandonar el planeta rojo cuando éste se encuentre 255º - 180º = 75º por delante de la Tierra. ¿Cada cuánto tiempo sucede esto? Nada más sencillo. Tan sólo hay que plantear las ecuaciones de los desplazamientos angulares (cinemática elemental del movimiento circular, de la que se estudia en el Bachillerato) para ambos planetas en función del tiempo.
Para Marte:
theta_M (t) = 44º + 0,524 (grados/día) t
Para la Tierra:
theta_T (t) = 0,986 (grados/día) t
Siempre que se cumpla la ecuación siguiente, la orientación de los dos planetas será la adecuada para el viaje de regreso:
theta_T (t) + 75º = theta_M (t) + 360º n
donde n es un número entero y positivo. La primera situación favorable se da cuando en la expresión anterior se hace n = 1, lo que sucede al cabo de unos 713 días medidos desde el comienzo de la misión, es decir, desde que la nave abandonase la Tierra. Esto significa que la tripulación deberá permanecer, al menos, 713 - 258 = 455 días sobre la superficie de Marte. La misión más corta en el tiempo posible durará 258 + 258 + 455 = 971 días, o lo que es lo mismo, unos 2,7 años. Podéis ahora comparar estos números con los que proporcionaba el astronauta Nicholas Willis al principio del post. Más aún, las estimaciones de la propia NASA son de 224 días para la ida y 237 para la vuelta, permaneciendo en Marte otros 458 días.
Obviamente los primeros (los de la película) no se ajustan demasiado bien a los que hemos obtenido, lo cual hace pensar que la expedición debe de seguir alguna órbita alternativa a la de Hohmann. Dicha trayectoria alternativa no va en contra de las leyes conocidas de la física, pero puede presentar otra serie de dificultades muy a tener en cuenta por los ingenieros y científicos encargados del diseño de la misión. En efecto, sería perfectamente posible trazar un plan que supusiese un tiempo de permanencia en la superficie de Marte mucho más reducida. Por ejemplo, si este lapso fuese de únicamente 30 días, la Tierra y Marte deberían estar separados por un ángulo de 46º en lugar de los 44º requeridos para la órbita de transferencia de Hohmann, haciendo que la ida durase 228 días (un mes menos, como no podía ser de otra manera) para que la vuelta comenzase en el mismo punto de la órbita en que tenía lugar la primera expedición que hemos analizado.
Sin embargo, el viaje de regreso no sería tan elemental y resultaría algo más complicado de calcular. Se requiere algo de teoría de cónicas y la 2ª ley de Kepler para determinar el tiempo de tránsito durante la vuelta, siempre dependiendo de la excentricidad de la órbita elíptica que debería seguir la nave espacial. Ésta podría ser tan excéntrica como para llegar incluso a acercarse hasta únicamente 45 millones de kilómetros del Sol, cerca del planeta Mercurio y atravesando igualmente la órbita de Venus. Diferentes valores seleccionados de las excentricidades de las órbitas para los viajes de regreso proporcionan distintos tiempos de permanencia de las tripulaciones sobre la superficie del planeta rojo. Ahora bien, puede que el equipo del control de la misión no los aprobase, ya que probablemente los valores de los "delta de v" fuesen excesivos. O quizá tampoco resultase demasiado razonable llevar a cabo una misión tan importante en la historia de la Humanidad para luego permanecer únicamente unas pocas semanas en Marte. Y más importante aún, el nivel de radiación o bombardeo de partículas subatómicas al que quedarían expuestos los astronautas podría superar los umbrales aconsejables para asegurar su integridad física. Tan sólo debéis pensar que una nave espacial que se acerque al Sol a una distancia similar a la que orbita Mercurio se verá bañado en casi 7 veces la cantidad de radiación que en la Tierra. ¿Qué agencia espacial asumiría este riesgo?
Fuentes:
Orbital Timing for a Mission to Mars. Stephen B. Turcotte. The Physics Teacher. Vol. 43, 293-296. May 2005.
Journey to Mars: the physics of travelling to the red planet. Arthur Stinner and John Begoray. Physics Education. Vol. 40(1), 35-45. May 2005.
Entradas
.png)
.PNG)
